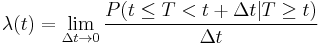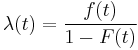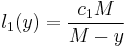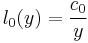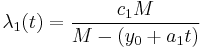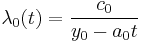Inhibition Theory
Inhibition theory is based on the basic assumption that, during the performance of any mental task, which requires a minimum of mental effort, the subject actually goes through a series of alternating states of distraction (non-work) and attention (work). These alternating states of distraction (state 0) and attention (state 1) are latent states, which cannot be observed and which are completely imperceptible to the subject. Additionally, the concept of inhibition or reactive inhibition is introduced, which is also latent. The assumption is made, that during states of attention inhibition linearly increases with a certain slope a1 and during states of distraction inhibition linearly decreases with a certain slope a0. According to this view the distraction states can be considered as a sort of recovery states. It is further assumed, that when the inhibition increases during a state of attention, depending on the amount of increase, the inclination to switch to a distraction state also increases and when the inhibition decreases during a state of distraction, depending on the amount of decrease, the inclination to switch to an attention state increases. The inclination to switch from one state to the other is mathematically described as a transition rate or hazard rate, which makes the whole process of alternating distraction times and attention times a stochastic process.
Theory
If one thinks of a non-negative continuous random variable T as representing the time until some event will take place then the hazard rate λ(t) for that random variable is defined to be the limiting value of the probability that the event will take place in a small interval [t,t+Δt], given the event has not occurred before time t, divided by Δt. Formally, the hazard rate is defined by the following limit:
The hazard rate λ(t) can also be written in terms of the density function or probability density function f(t) and the distribution function or cumulative distribution function F(t):
The transition rates λ1(t), from state 1 to state 0, and λ0(t), from state 0 to state 1, depend on inhibition Y(t): λ1(t) = l1(Y(t)) and λ0(t) = l0(Y(t)), where l1 is a non-decreasing function and l0 is a non-increasing function. Note, that l1 and l0 are dependent on Y, whereas Y is dependent on T. Specification of the functions l1 and l0 leads to the various inhibition models. What can be observed in the test are the actual reaction times. A reaction time is the sum of a series of alternating distraction times and attention times, which both cannot be observed. However, it is nevertheless possible to estimate from the observable reaction times some properties of the latent process of distraction times and attention times, such as the average distraction time, the average attention time and the ratio a1/a0. In order to be able to simulate the consecutive reaction times, inhibition theory has been specified into various inhibition models. One is the so-called beta inhibition model. In the beta-inhibition model, it is assumed that the inhibition Y(t) oscillates between two boundaries which are 0 and M (M for Maximum), where M is positive. In this model l1 and l0 are as follows:
and
both with c0 > 0 and c1 > 0. Note that, according to the first assumption, as y goes to M (during a interval), l1(y) goes to infinity and this forces a transition to a state of rest before the inhibition can reach M. Note further that, according to the second assumption, as y goes to zero (during a distraction), l0(y) goes to infinity and this forces a transition to a state of work before the inhibition can reach zero. For a work interval starting at t0 with inhibition level y0=Y(t0) the transition rate at time t0+t is given by λ1(t) = l1(y0+a1t). For a non-work interval starting at t0 with inhibition level y0=Y(t0) the transition rate is given by λ0(t) = l0(y0-a0t). Therefore
and
The model has Y fluctuating in the interval between 0 and M. The stationary distribution of Y/M in this model is a beta distribution (reason to call it the beta inhibition model).
The total real working time until the conclusion of the task (or the task unit in case of a repetition of equivalent unit tasks, such as is the case in the Attention Concentration Test is referred to as A. The average stationary response time E(T) may written as
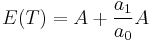 .
.
For M goes to infinity λ1(t) = c1. This model is known as the gamma - or Poisson inhibition model (see Smit and van der Ven, 1995).
Application
Inhibition theory has especially been developed to account for the short-term oscillation as well as the long-term trend in the reaction time curves obtained in continuous response tasks such as the Attention Concentration Test. The Attention Concentration Test typically consists of an overlearned prolonged work task in which each response elicits the next. Several authors, among them Binet (1900), stressed the importance of the fluctuation in the reaction times suggesting the mean deviation as a measure of performance. In this connection it is also worthwhile to mention a study by Hylan (1898). He used, in his experiment B, a 27 single digits addition task. He not only pointed to the importance of the fluctuation of reaction times, but he was also the first one who reported gradually increasing (marginally decreasing) reaction time curves (Hylan, 1898, page 15, figure 5).
Recently, the inhibition model has been used also to explain the phase durations in binocular rivalry experiments (van der Ven, Gremmen & Smit, 2005). The model is capable to account for the statistical properties of the alternating phase durations
T11, T01, T12 ,T02, T13, T03, ...,
representing the amounts of time a person perceives the stimulus in one eye T1j and in the other eye T0j.
References
- Binet, A. (1900). Attention et adaptation [Attention and adaptation]. L'annee psychologique, 6, 248-404.
- Hylan, J.P. (1898). The Fluctuation of Attention. The Psychological Review, Series of Monograph Supplements, Vol. II., No. 2 (Whole No. 6). New York: The MacMillan Company.'
- Smit, J.C. and van der Ven, A.H.G.S. (1995). Inhibition in Speed and Concentration Tests: The Poisson Inhibition Model. Journal of Mathematical Psychology, 39, 265-273.
- Ven, A.H.G.S. van der, Gremmen, F.M. and Smit, J.C. (2005). A Statistical Model for Binocular Rivalry. British Journal of Mathematical and Statistical Psychology, 58, 97-116.